AcWing 1064. 小国王【线性状压DP+目标状态优化】
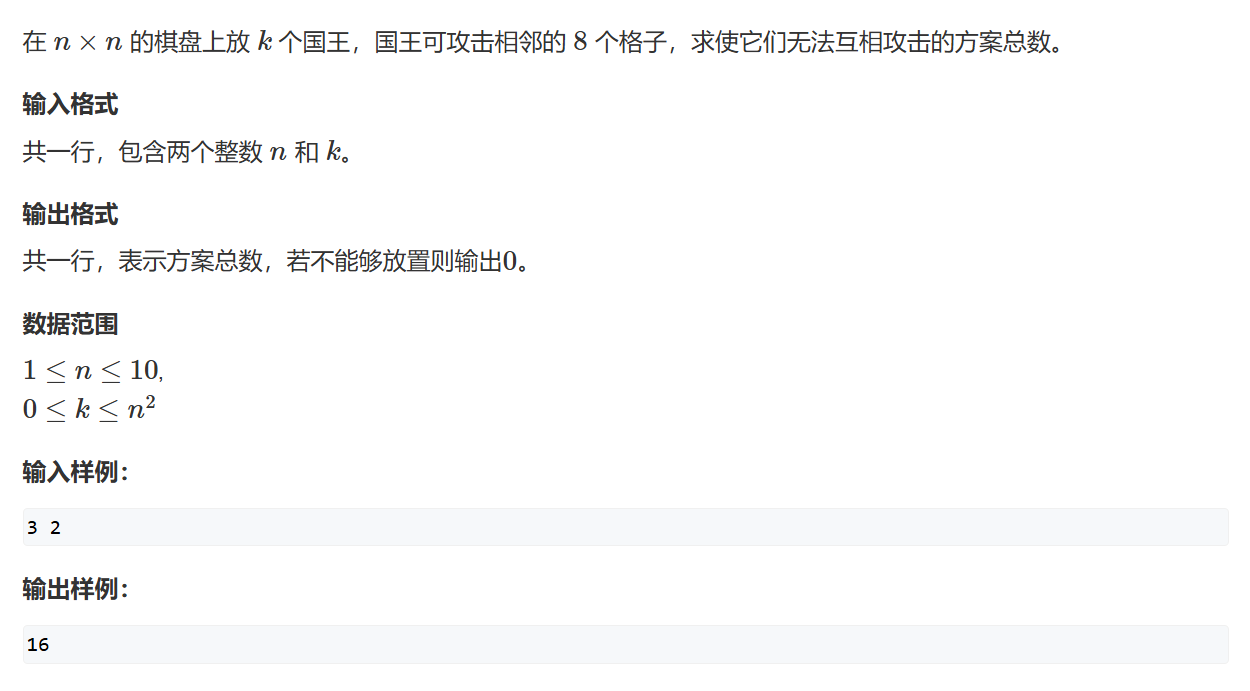
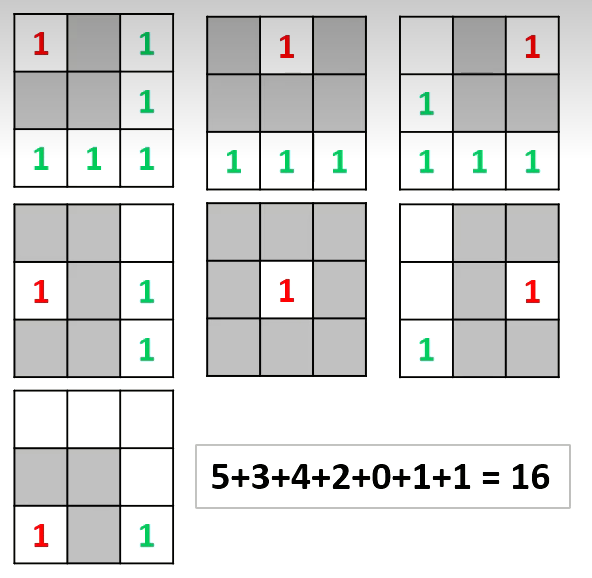
#include<bits/stdc++.h>
using namespace std;
#define int long long
const int N=1e5+10;
const int mod=1e9+7;
int n,k;
int cnt[N];
int dp[12][110][3000];
vector<int>head[N];
vector<int>state;
bool check(int st){
for(int i=0;i<n;i++)
if((st>>i&1)&&st>>(i+1)&1) return 0;
return 1;
}
int count(int st){
int res=0;
for(int i=0;i<n;i++){
res+=st>>i&1;
}
return res;
}
void solve(){
cin>>n>>k;
for(int i=0;i<1<<n;i++){
if(check(i)) state.push_back(i);
cnt[i]=count(i);
}
for(int i=0;i<state.size();i++){
for(int j=0;j<state.size();j++){
int x=state[i],y=state[j];
if(((x&y)==0)&&check(x|y)) head[i].push_back(j);
}
}
dp[0][0][0]=1;
for(int i=1;i<=n+1;i++){
for(int j=0;j<=k;j++){
for(int a=0;a<state.size();a++){
for(int b:head[a]){
int c=cnt[state[a]];
if(j>=c){
dp[i][j][a]+=dp[i-1][j-c][b];
}
}
}
}
}
cout<<dp[n+1][k][0]<<endl;
}
signed main(){
int t=1;
//cin>>t;
while(t--){
solve();
}
}
AcWing 327. 玉米田【线性状压DP+目标状态优化】

#include<bits/stdc++.h>
using namespace std;
#define int long long
const int N=1e5+10;
const int mod=1e8;
int n,k;
int cnt[N],a[110];
int dp[14][1<<14];
vector<int>head[1<<14];
vector<int>state;
bool check(int st){
return !(st&st<<1);
}
int count(int st){
int res=0;
for(int i=0;i<n;i++){
res+=st>>i&1;
}
return res;
}
void solve(){
int n,m;
cin>>n>>m;
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
cin>>k,a[i]|=!k<<(j-1);
}
}
for(int st=0;st<1<<m;st++){
if(check(st)) state.push_back(st);
}
for(auto it:state){
for(auto next_it:state){
if(!(it&next_it)) head[it].push_back(next_it);
}
}
dp[0][0]=1;
for(int i=1;i<=n+1;i++){
for(auto st:state){
if(!(st&a[i])){
for(auto next_st:head[st]){
dp[i][st]+=dp[i-1][next_st];
dp[i][st]%=mod;
}
}
}
}
cout<<dp[n+1][0]<<endl;
}
signed main(){
int t=1;
//cin>>t;
while(t--){
solve();
}
}
[NOI2001] 炮兵阵地
题目描述
司令部的将军们打算在 $N\times M$ 的网格地图上部署他们的炮兵部队。
一个 $N\times M$ 的地图由 $N$ 行 $M$ 列组成,地图的每一格可能是山地(用 $\texttt{H}$ 表示),也可能是平原(用 $\texttt{P}$ 表示),如下图。
在每一格平原地形上最多可以布置一支炮兵部队(山地上不能够部署炮兵部队);一支炮兵部队在地图上的攻击范围如图中黑色区域所示:
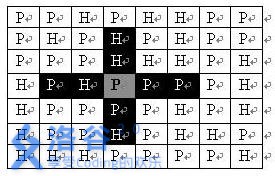
如果在地图中的灰色所标识的平原上部署一支炮兵部队,则图中的黑色的网格表示它能够攻击到的区域:沿横向左右各两格,沿纵向上下各两格。
图上其它白色网格均攻击不到。从图上可见炮兵的攻击范围不受地形的影响。
现在,将军们规划如何部署炮兵部队,在防止误伤的前提下(保证任何两支炮兵部队之间不能互相攻击,即任何一支炮兵部队都不在其他支炮兵部队的攻击范围内),在整个地图区域内最多能够摆放多少我军的炮兵部队。
样例输入 #1
5 4
PHPP
PPHH
PPPP
PHPP
PHHP
样例输出 #1
6
#include<bits/stdc++.h>
using namespace std;
#define int long long
const int N=1e5+10;
const int mod=1e9+7;
int n,m;
char c;
int cnt[N],g[110];
int dp[2][1<<10][1<<10];
vector<int>head[N];
vector<int>state;
bool check(int st){
return !(st&st>>1||st&st>>2);
}
int count(int st){
int res=0;
for(int i=0;i<m;i++){
res+=st>>i&1;
}
return res;
}
void solve(){
cin>>n>>m;
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
cin>>c, g[i]|=(c=='H')<<(j-1);
}
}
for(int st=0;st<1<<m;st++){
if(check(st)) state.push_back(st),cnt[st]=count(st);
}
for(int x: state){
for(int y: state){
if(!(x&y)) head[x].push_back(y);
}
}
for(int i=1;i<=n+2;i++){
for(int st:state){
if(!(st&g[i])){
for(int p1:head[st]){
for(int p2:head[p1]){
if(!(st&p2)){
dp[i&1][st][p1]=max(dp[i&1][st][p1],dp[i-1&1][p1][p2]+cnt[st]);
}
}
}
}
}
}
cout<<dp[n+2&1][0][0]<<endl;
}
signed main(){
int t=1;
//cin>>t;
while(t--){
solve();
}
}
