• 树的最长路径
  • 题目
  • 思路
  • 代码

树的最长路径

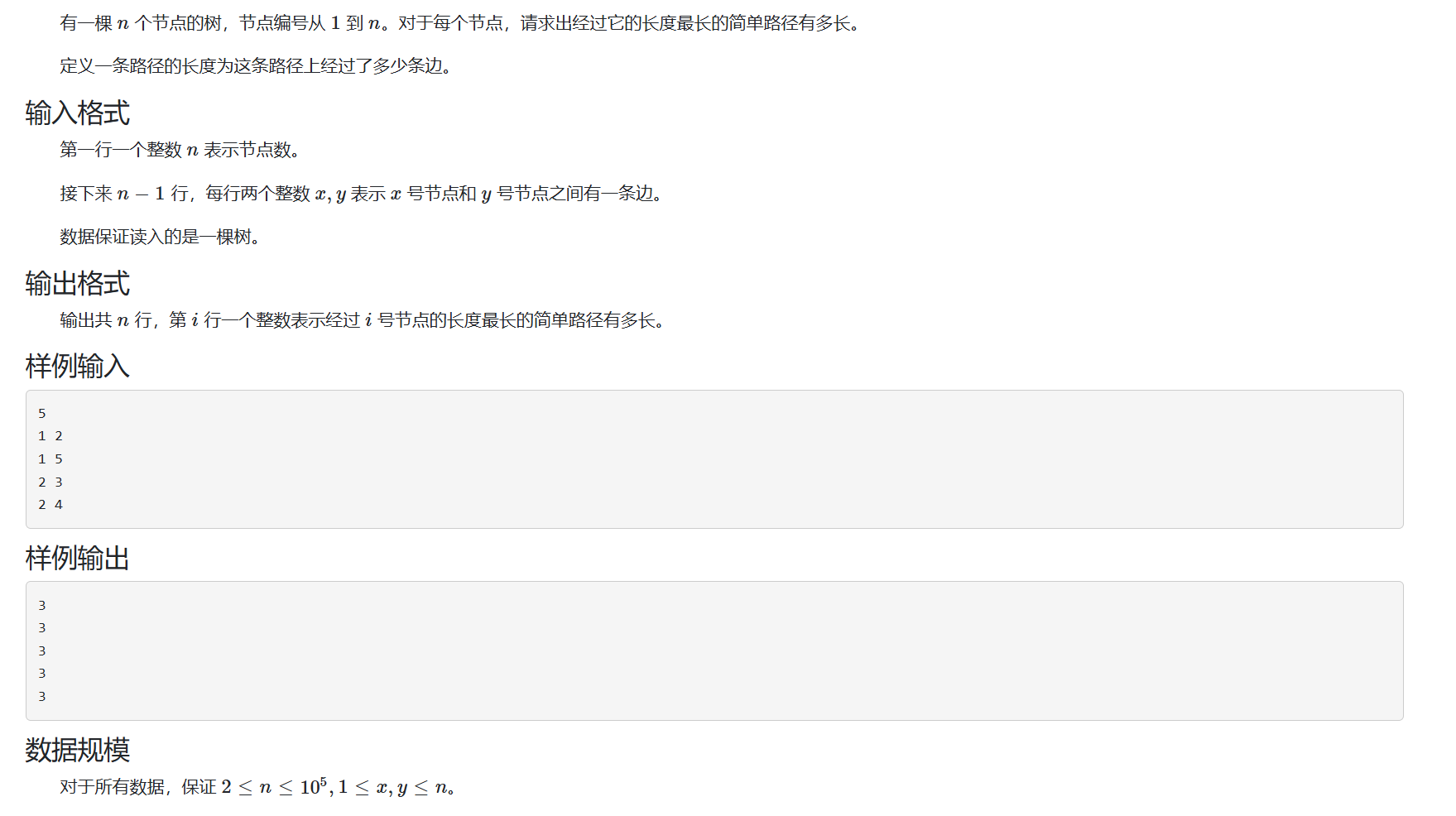
题目

思路

这道题的前置知识点可以参考[树的最长路径](1072. 树的最长路径 - AcWing题库)easy版，核心代码如下：

void up(int u,int fa){
    st[u]=1;
    for(auto v:e[u]){
        if(v.to==fa) continue;
        up(v.to,u);
        if(f[u][1]<=f[v.to][1]+v.w){
            f[u][2]=f[u][1];
            f[u][1]=f[v.to][1]+v.w;
        }
        else if(f[u][2]<=f[v.to][1]+v.w){
            f[u][2]=f[v.to][1]+v.w;
        }
    }
}

以某点为根的子树的最长路径即为以该点为根的最长路与次长路的长度和，一遍dfs即可求出所有子树的最长路径，但在这个题里，显然某点的最长路径不一定存在于某点的子树中，而存在于该点的根节点里面，这个时候就需要引入换根的概念了

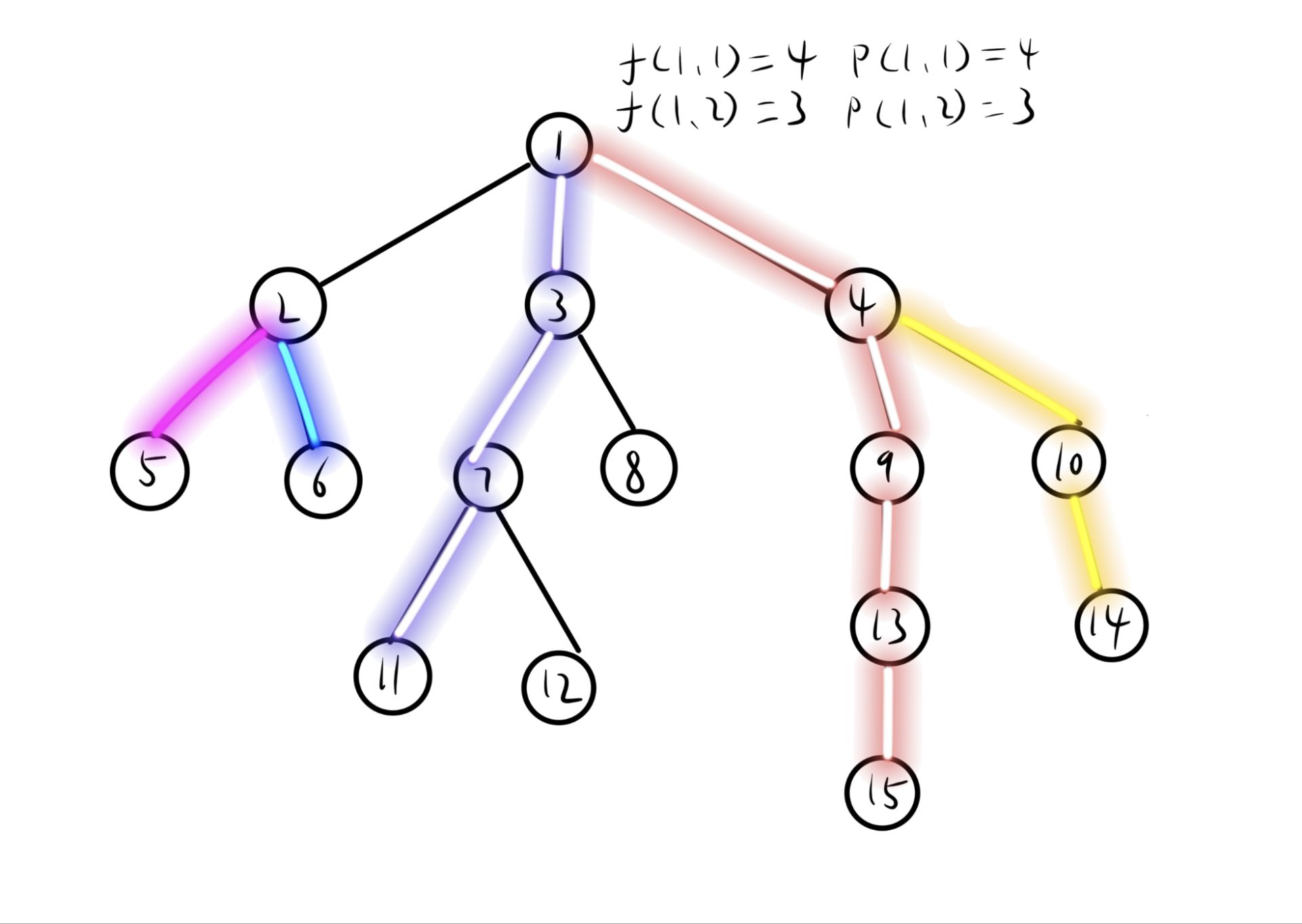
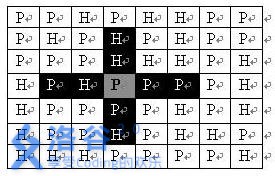
​ 如图给出了一颗树，当以1为根时，显然他的最长直径为路径1-3-7-11（f[1] [2]=3,一维表示以1为根，二维表示第2长的路）与路径1-4-9-13-15（f[1] [1]=4）的长度和7.

​ 但当我们考虑结点4时,第一遍dfs跑出来的结果p[4] [1]=3,p[4] [2]=2,显然不是最优的，因为把结点1看作他的子节点时，f[4] [1]可以被f[1] [2]+1替换，同理f[3] [1]可以被f[1] [1]+1替换，f[3] [2]继承 f[3] [1]。

​ 如果此时我们对每个节点都跑一遍dfs的话可以解决这个问题，但其时间复杂度为O(n^2) 的，显然不符合题面的要求，所有需要考虑怎么在O(n)的时间复杂度下得出每点的答案，这个时候对每个结点观察可以看出，答案是否需要更新只和他的根节点信息有关，当根节点长度大于p[i][1]或者p[i][2]时按需求更新答案即可。

​ 具体的更新答案的情况有两类，一种是子节点v被父节点u的第一长路径覆盖，另一种则是被第二长路径覆盖或不被覆盖。

​ 当我们考虑第一种情况是，对应图中的v=4号结点，当前结点v被根节点u的第一长的路径包括在内，v的第一长的路径长度一定是最优的，但需要考虑f[v] [2]与f[u] [2]+1的关系。第二种情况对应v=2或者v=3，此时根节点u中一定存在一条最优的路径大于p[v] [1]与p[v] [2]，因为根结点在寻找最长路径时没有考虑经过子节点v，所以子节点v中的任何路径都是非最优解，那么直接将p[v] [2]更新为p[v] [1],并用p[u] [1]+1替换p[v] [1]。

​ 注意在每一次更新都要维护当前的结点所选的每一条路都要经过的那个子节点，用来后续判断某个点是否为父节点所选

代码

#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N = 2e6 + 10;
typedef pair<int,int> PII;
bool st[N];
struct tree{
    int to;
};
int size[N],f[N][3],p[N][3];
vector<tree> e[N];
void up(int u){
    st[u]=1;
    for(auto v:e[u]){
        if(st[v.to]) continue;
        up(v.to);
        if(f[u][1]<f[v.to][1]+1){
            f[u][2]=f[u][1];
            p[u][2]=p[u][1];
            f[u][1]=f[v.to][1]+1;
            p[u][1]=v.to;
        }
        else if(f[u][2]<f[v.to][1]+1){
            f[u][2]=f[v.to][1]+1;
            p[u][2]=v.to;
        }
    }
}
void down(int u){
    st[u]=1;
    for(auto v:e[u]){
        if(st[v.to]) continue;
        if(p[u][1]==v.to){
            if(f[v.to][1]<f[u][2]+1){
                f[v.to][2]=f[v.to][1];
                p[v.to][2]=p[v.to][1];
                f[v.to][1]=f[u][2]+1;
                p[v.to][1]=u;
            }
            else if(f[v.to][2]<f[u][2]+1){
                f[v.to][2]=f[u][2]+1;
                p[v.to][2]=u;
            }
        }
        else{
            f[v.to][2]=f[v.to][1];
            p[v.to][2]=p[v.to][1];
            f[v.to][1]=f[u][1]+1;
            p[v.to][1]=u;
        }
        down(v.to);
    }
}
void solve(){
    int n;
    cin>>n;
    for(int i=1;i<n;i++){
        int u,v;
        cin>>u>>v;
        e[u].push_back({v});
        e[v].push_back({u});
    }
    up(1);
    for(int i=1;i<=n;i++) st[i]=0;
    down(1);
    int ans=0;
    for(int i=1;i<=n;i++){
        cout<<f[i][1]+f[i][2]<<endl;
    }
}
signed main(){
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    int t=1;
    //cin >> t;
    while (t--) {
        solve();
    } 
}

D - Buildings

Problem Statement

There are $N$ buildings, Building $1$, Building $2$, $\ldots$, Building $N$, arranged in a line in this order. The height of Building $i$ $(1 \leq i \leq N)$ is $H_i$.

For each $i = 1, 2, \ldots, N$, find the number of integers $j$ $(i < j \leq N)$ satisfying the following condition:

• There is no building taller than Building $j$ between Buildings $i$ and $j$.

Constraints

• $1 \leq N \leq 2 \times 10^5$
• $1 \leq H_i \leq N$
• $ H_i\neq H_j\ (i\neq j)$
• All input values are integers.

Sample Input 1

5
2 1 4 3 5

Sample Output 1

3 2 2 1 0

For $i=1$, the integers $j$ satisfying the condition are $2$, $3$, and $5$: there are three. (Between Buildings $1$ and $4$, there is a building taller than Building $4$, which is Building $3$, so $j=4$ does not satisfy the condition.) Therefore, the first number in the output is $3$.

实现

倒着将元素挨个放入单调栈，栈的元素个数即为当前位置的答案

#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N = 2e5 + 10;
int a[N],b[N],c[N];
stack<int>st;
void solve(){
    int n;
    cin>>n;
    for(int i=1;i<=n;i++){
        cin>>a[i];
    }
    for(int i=n;i>=1;i--){     
        b[i]=st.size();
        while(!st.empty()&&a[i]>st.top()){
            st.pop();
        }
        st.push(a[i]);
    }
    for(int i=1;i<=n;i++){
        cout<<b[i]<<' ';
    }
    cout<<endl;
}
signed main() {
    int t=1;
    //cin >> t;
    while (t--) {
        solve();
    }
       
}

E - K-th Largest Connected Components

Problem Statement

There is an undirected graph with $N$ vertices and $0$ edges. The vertices are numbered $1$ to $N$.

You are given $Q$ queries to process in order. Each query is of one of the following two types:

• Type $1$: Given in the format 1 u v. Add an edge between vertices $u$ and $v$.

• Type $2$: Given in the format 2 v k. Print the $k$-th largest vertex number among the vertices connected to vertex $v$. If there are fewer than $k$ vertices connected to $v$, print -1.

Constraints

• $1 \leq N, Q \leq 2 \times 10^5$
• In a Type $1$ query, $1 \leq u < v \leq N$.
• In a Type $2$ query, $1 \leq v \leq N$, $1 \leq k \leq 10$.
• All input values are integers.

Sample Input 1

4 10
1 1 2
2 1 1
2 1 2
2 1 3
1 1 3
1 2 3
1 3 4
2 1 1
2 1 3
2 1 5

Sample Output 1

2
1
-1
4
2
-1

• In the first query, an edge is added between vertices $1$ and $2$.
• In the second query, two vertices are connected to vertex $1$: $1$ and $2$. Among them, the $1$-st largest vertex number is $2$, which should be printed.
• In the third query, two vertices are connected to vertex $1$: $1$ and $2$. Among them, the $2$-nd largest vertex number is $1$, which should be printed.
• In the fourth query, two vertices are connected to vertex $1$: $1$ and $2$, which is fewer than $3$, so print -1.
• In the fifth query, an edge is added between vertices $1$ and $3$.
• In the sixth query, an edge is added between vertices $2$ and $3$.
• In the seventh query, an edge is added between vertices $3$ and $4$.
• In the eighth query, four vertices are connected to vertex $1$: $1,2,3,4$. Among them, the $1$-st largest vertex number is $4$, which should be printed.
• In the ninth query, four vertices are connected to vertex $1$: $1,2,3,4$. Among them, the $3$-rd largest vertex number is $2$, which should be printed.
• In the tenth query, four vertices are connected to vertex $1$: $1,2,3,4$, which is fewer than $5$, so print -1.

实现

启发式合并+平衡树查询

#include <bits/stdc++.h>
#include <bits/extc++.h>
using namespace __gnu_cxx;
using namespace __gnu_pbds;
using namespace std;
#define int long long
typedef tree<int, null_type, greater<int>, rb_tree_tag, tree_order_statistics_node_update> Tree;
const int N = 2e6 + 10;
Tree tr[N];
int f[N];
int find(int x){
    return f[x]==x?x:f[x]=find(f[x]);
}
void solve(){
    int n,q;
    cin>>n>>q;
    for(int i=1;i<=n;i++){
        tr[i].insert(i);
        f[i]=i;
    }
    for(int i=1;i<=q;i++){
        int st;
        cin>>st;
        if(st==1){
            int u,v;
            cin>>u>>v;
            u=find(u),v=find(v);
            if(u==v) continue;
            if(tr[u].size()>tr[v].size()){
                swap(u,v);
            }
            for(auto it:tr[u]){
                tr[v].insert(it);
                f[it]=v;
            }
            tr[u].clear();
        }
        else{
            int v,k;
            cin>>v>>k;
            v=find(v);
            if(tr[v].size()>=k){
                cout<<*tr[v].find_by_order(k-1)<<endl;
            }
            else{
                cout<<-1<<endl;
            }
        }
    }
}
signed main(){
    int t=1;
    //cin >> t;
    while (t--) {
        solve();
    } 
}

琪露诺

在幻想乡，琪露诺是以笨蛋闻名的冰之妖精。

某一天，琪露诺又在玩速冻青蛙，就是用冰把青蛙瞬间冻起来。但是这只青蛙比以往的要聪明许多，在琪露诺来之前就已经跑到了河的对岸。于是琪露诺决定到河岸去追青蛙。

小河可以看作一列格子依次编号为 $0$ 到 $N$，琪露诺只能从编号小的格子移动到编号大的格子。而且琪露诺按照一种特殊的方式进行移动，当她在格子 $i$ 时，她只移动到区间 $[i+L,i+R]$ 中的任意一格。你问为什么她这么移动，这还不简单，因为她是笨蛋啊。

每一个格子都有一个冰冻指数 $A_i$，编号为 $0$ 的格子冰冻指数为 $0$。当琪露诺停留在那一格时就可以得到那一格的冰冻指数 $A_i$。琪露诺希望能够在到达对岸时，获取最大的冰冻指数，这样她才能狠狠地教训那只青蛙。

但是由于她实在是太笨了，所以她决定拜托你帮它决定怎样前进。

开始时，琪露诺在编号 $0$ 的格子上，只要她下一步的位置编号大于 $N$ 就算到达对岸。

样例输入 #1

5 2 3
0 12 3 11 7 -2

样例输出 #1

11

#include <bits/stdc++.h>
using namespace std;
#define int long long
#define endl '\n' 
const int N=2e6;
int a[N],dp[N],s[N];
deque<int>dq1,dq2;
int n,h;
deque<int>p;         
void solve(){
    int n,l,r;
    cin>>n>>l>>r;
    for(int i=0;i<=n;i++){
        cin>>a[i];
    }
    memset(dp,-127,sizeof(dp));
    int j=0;
    dp[0]=0;
    for(int i=l;i<=n;i++){
        while(j<=i-l){
            while(!p.empty()&&dp[j]>=dp[p.back()]){
                p.pop_back();
            }
            p.push_back(j);
            j++;
        }
        if(!p.empty()&&p.front()<i-r) p.pop_front();
        dp[i]=dp[p.front()]+a[i];
    }
    int ans=-1e9;
    for(int i=n-r+1;i<=n;i++){
       ans=max(ans,dp[i]);
    }
    cout<<ans<<endl;

}

signed main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout << fixed << setprecision(12);
    int t=1;
    //cin>>t;
    while(t--){
        solve();
    }
}

[NOIP2017 普及组] 跳房子

跳房子，也叫跳飞机，是一种世界性的儿童游戏，也是中国民间传统的体育游戏之一。

跳房子的游戏规则如下：

在地面上确定一个起点，然后在起点右侧画 $n$ 个格子，这些格子都在同一条直线上。每个格子内有一个数字（整数），表示到达这个 格子能得到的分数。玩家第一次从起点开始向右跳，跳到起点右侧的一个格子内。第二次再从当前位置继续向右跳，依此类推。规则规定：

玩家每次都必须跳到当前位置右侧的一个格子内。玩家可以在任意时刻结束游戏，获得的分数为曾经到达过的格子中的数字之和。

现在小 R 研发了一款弹跳机器人来参加这个游戏。但是这个机器人有一个非常严重的缺陷，它每次向右弹跳的距离只能为固定的 $d$。小 R 希望改进他的机器人，如果他花 $g$ 个金币改进他的机器人，那么他的机器人灵活性就能增加 $g$，但是需要注意的是，每 次弹跳的距离至少为 $1$。具体而言，当 $g<d$ 时，他的机器人每次可以选择向右弹跳的距离为 $d-g,d-g+1,d-g+2,\ldots,d+g-1,d+g$；否则当 $g \geq d$ 时，他的机器人每次可以选择向右弹跳的距离为 $1,2,3,\ldots,d+g-1,d+g$。

现在小 R 希望获得至少 $k$ 分，请问他至少要花多少金币来改造他的机器人。

若无论如何他都无法获得至少 $k$ 分，输出 $-1$。

样例输入 #1

7 4 10
2 6
5 -3
10 3
11 -3
13 1
17 6
20 2

样例输出 #1

2

#include <bits/stdc++.h>
using namespace std;
#define int long long
#define endl '\n' 
const int N=2e6;
int n,d,k;
int x[N],s[N];
int dp[N];
deque<int>p;         
bool check(int mid){
    memset(dp,-127,sizeof(dp));
    p.clear();
    int l=max((int)1,d-mid);
    int r=min(d+mid,x[n]);
    int idx=0;
    int num=0;
    dp[0]=0;
    for(int i=1;i<=n;i++){
        if(x[i]>=l&&x[i]<=r){
            idx=i;
            dp[idx]=s[idx];
            num=dp[idx];
            break;
        }
    }
    if(idx==0) return 0;
    for(int i=2;i<=n;i++){
        while(x[idx]<=x[i]-l){
            while(!p.empty()&&dp[idx]>=dp[p.back()]){
                p.pop_back();
            }
            p.push_back(idx);
            idx++;
        }
        while(!p.empty()&&x[p.front()]<x[i]-r) p.pop_front();
        if(!p.empty())
            dp[i]=dp[p.front()]+s[i];
        num=max(num,dp[i]);
    }
    if(num>=k) return 1;
    else return 0;
}
void solve(){
    cin>>n>>d>>k;
    for(int i=1;i<=n;i++){
        cin>>x[i]>>s[i];
    }
    int l=0;
    int r=1e9;
    while(l<r){
        int mid=l+r>>1;
        if(check(mid)) r=mid;
        else l=mid+1;
    }
    if(l>=1e9) l=-1;
    cout<<l<<endl;
}

signed main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout << fixed << setprecision(12);
    int t=1;
    while(t--){
        solve();
    }
}

切蛋糕

今天是小 Z 的生日，同学们为他带来了一块蛋糕。这块蛋糕是一个长方体，被用不同色彩分成了 $n$ 个相同的小块，每小块都有对应的幸运值。

小 Z 作为寿星，自然希望吃到的蛋糕的幸运值总和最大，但小 Z 最多又只能吃 $m(m\le n)$ 小块的蛋糕。

请你帮他从这 $n$ 小块中找出连续的 $k(1 \le k\le m)$ 块蛋糕，使得其上的总幸运值最大。

形式化地，在数列 ${p_n}$ 中，找出一个子段 $[l,r](r-l+1\le m)$，最大化 $\sum\limits_{i=l}^rp_i$。

样例输入 #1

5 2
1 2 3 4 5

样例输出 #1

9

#include <bits/stdc++.h>
using namespace std;
#define int long long
#define endl '\n' 
const int N=2e6;
int a[N],dp[N],s[N];
deque<int>dq1,dq2;
int n,h;
deque<int>p;         
void solve(){
   int n,m;
   cin>>n>>m;
   int ans=0;
   for(int i=1;i<=n;i++){
       cin>>a[i];
       s[i]=s[i-1]+a[i];
    }
    int j=1;
    for(int i=1;i<=n;i++){
        while(j<=min(i+m-1,n)){
            while(!p.empty()&&s[j]>=s[p.back()]){
                p.pop_back();
            }
            p.push_back(j);
            j++;
        }
        if(p.front()<i) p.pop_front();
        ans=max(ans,s[p.front()]-s[i-1]);
    }
    cout<<ans<<endl;
}

signed main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout << fixed << setprecision(12);
    int t=1;
    //cin>>t;
    while(t--){
        solve();
    }
}

D. Chat Program

题目

You’re the researcher of the International Chat Program Company (ICPC). Today, you discover the following chat history when reviewing some research data.

SUA (2022/12/04 23:01:25)

I’m out of ideas for competitive programming problems! Please give me a problem about sequences.

BOT (2022/12/04 23:01:27)

Sure. Here is a competitive programming problem about sequences.

Given an integer sequence $a_1, a_2, \cdots, a_n$ of length $n$ and four other integers $k$, $m$, $c$ and $d$, your goal is to maximize the $k$-th largest element in the sequence.

To achieve the goal, you can perform the following operation at most once: select a continuous sub-array of length $m$ and add an arithmetic sequence with length $m$, initial term $c$ and common difference $d$ to the sub-array.

More formally, you can select an integer $p$ satisfying $1 \le p \le n - m + 1$ and add $(c + di)$ to $a_{p + i}$ for all $0 \le i < m$.

Calculate the largest possible value of the $k$-th largest element in the sequence after at most one operation.

The $k$-th largest element in the sequence is the $k$-th element in the sorted sequence after sorting all elements from the largest to the smallest. For example, the $3$rd largest element in sequence ${5, 7, 1, 9}$ is $5$, while the $3$rd largest element in sequence ${9, 7, 5, 9}$ is $7$.

SUA (2022/12/05 00:15:17)

This problem seems difficult! Please teach me the solution.

BOT (2022/12/05 00:15:30)

Sure. Firstly, we can…

[DATA EXPUNGED]

Unfortunately, parts of the chat history are lost due to a disk failure. You’re amazed at how a chat program can create a competitive programming problem. To verify whether the chat program can create valid problems, you decide to try on this problem.

思路

二分答案，如果一个数想成为数组中的第k大，那么就需要至少k-1个比他大的数存在，在check函数中，我们把比mid大的数字状态更新为1，不做考虑，所有状态为0的点在need数组中记录达到mid所需要的最小项数，现在要做的就是维护所有状态为0的点，让他们尽可能多的变成比mid大的数字，当这些数字满足>=k时，则当前的mid是满足条件的

因为等差数列是连续加在数组上的，那么不妨把这个等差数列想象成一个滑动窗口m，m的第i个数代表等差数列的第i项，在移动窗口的时候窗口尾部每扫描到一个为0的点，判断一下他的need是否小于m的尾项，如果是，就加入到一个优先队列里面（优先队列用来存储当前元素弹出的下标idx，根据idx的大小关系排序，越小的弹出时间越早），否则直接略过，在每一次挪动窗口加入值之后用while循环判断当前有多少元素已经不满足条件。遍历一遍维护优先队列的最大size即可，加上之前已经大于mid的元素个数与k进行比较。

#include<bits/stdc++.h>
using namespace std;
#define int long long
const int N=2e5+10;
int n,k,m,c,d,a[N];
bool st[N];
int need[N];
bool check(int mid){
    for(int i=1;i<=n;i++){  
        if(a[i]>=mid) st[i]=1;
        else st[i]=0;
        need[i]=0;
    }
    for(int i=1;i<=n;i++){
        if(!st[i]){
            if(mid-a[i]<=c) need[i]=1;
            else{
                if(d==0) need[i]=1e9; //公差为0时，首项不满足，之后任何一项都不会满足，所以need[i]记录无限大
                else
                need[i]=(mid-a[i]-c+(d-1))/d+1; 
            }
        }
    }
    priority_queue<int,vector<int>,greater<int>>q;
    for(int i=1;i<=m;i++){
        if(st[i]==0&&need[i]<=i) q.push(m+(i-need[i])+1);
    }
    int ans=q.size();
    for(int i=m+1;i<=n;i++){
        if(st[i]==0&&need[i]<=m) q.push(i+(m-need[i])+1);
        while(!q.empty()&&q.top()<=i){
            q.pop();
        }
        ans=max(ans,(int)q.size());
    }
    for(int i=1;i<=n;i++){
        if(st[i]) ans++;
    }
    if(ans>=k) return 0;
    else return 1;
}
void solve()
{
    cin>>n>>k>>m>>c>>d;
    for(int i=1;i<=n;i++){
        cin>>a[i];
    }
    int l=0,r=1e17;
    while(l<r){
        int mid=l+r+1>>1;
        if(check(mid)) r=mid-1;
        else l=mid;
    }
    cout<<l<<endl;
}
signed main()
{
    int t=1;
    while(t--)
    {
        solve();
    }
}

C. Lazy Narek

题目

Narek is too lazy to create the third problem of this contest. His friend Artur suggests that he should use ChatGPT. ChatGPT creates $n$ problems, each consisting of $m$ letters, so Narek has $n$ strings. To make the problem harder, he combines the problems by selecting some of the $n$ strings possibly none and concatenating them without altering their order. His chance of solving the problem is defined as $score_n - score_c$, where $score_n$ is Narek’s score and $score_c$ is ChatGPT’s score.

Narek calculates $score_n$ by examining the selected string (he moves from left to right). He initially searches for the letter $\texttt{“n”}$, followed by $\texttt{“a”}$, $\texttt{“r”}$, $\texttt{“e”}$, and $\texttt{“k”}$. Upon finding all occurrences of these letters, he increments $score_n$ by $5$ and resumes searching for $\texttt{“n”}$ again (he doesn’t go back, and he just continues from where he left off).

After Narek finishes, ChatGPT scans through the array and increments $score_c$ by $1$ for each letter $\texttt{“n”}$, $\texttt{“a”}$, $\texttt{“r”}$, $\texttt{“e”}$, or $\texttt{“k”}$ that Narek fails to utilize (note that if Narek fails to complete the last occurrence by finding all of the $5$ letters, then all of the letters he used are counted in ChatGPT’s score $score_c$, and Narek doesn’t get any points if he doesn’t finish finding all the 5 letters).

Narek aims to maximize the value of $score_n - score_c$ by selecting the most optimal subset of the initial strings.

实现

定义dp[i] [j]为前i个字符串，最后一个字符串匹配到了j个字母（n–1,a–2,r–3,e–4,k–5），每一次更新当前字符串分别以前某个字符串需要的字母为开头开始计数，算出以这个字母开头的分数差，进行状态转移，最后在dp[n] [i]中枚举一下最优解减去i+1即为答案

#include<bits/stdc++.h>
using namespace std;
#define int long long
const int N=2e3+10;
int a[N],b[N],ans;
int dp[N][6];
int sum[6],need[6];
map<char,bool>st;

string temp="?narek";
int n,m;
void init(string s){
    for(int i=1;i<=5;i++) sum[i]=0,need[i]=i;
    for(int i=1;i<=m;i++){
        if(st[s[i]]){
            for(int j=1;j<=5;j++){
                if(s[i]==temp[need[j]]){
                    need[j]++;
                    if(need[j]==6) sum[j]+=5,need[j]=1;
                }
                else sum[j]--;
            }
        }
    }
}
void solve()
{
    cin>>n>>m;
    for(int i=0;i<=n;i++){
        for(int j=1;j<=6;j++){
            dp[i][j]=-1e4;
        }
    }
    dp[0][1]=0;
    for(int i=1;i<=n;i++){
        string s;
        cin>>s;
        s=' '+s;
        init(s);
        for(int j=1;j<=5;j++) dp[i][j]=dp[i-1][j];
        for(int j=1;j<=5;j++) dp[i][need[j]]=max(dp[i][need[j]],dp[i-1][j]+sum[j]);
    }
    int ans=0;
    for(int i=1;i<=5;i++){
        ans=max(ans,dp[n][i]-i+1);
    }
    cout<<ans<<endl;
}
signed main()
{
    st['n']=1,st['a']=1,st['r']=1,st['e']=1,st['k']=1;
    int t=1;
    cin>>t;
    while(t--)
    {
        solve();
    }
}

低价购买

题目描述

“低价购买”这条建议是在奶牛股票市场取得成功的一半规则。要想被认为是伟大的投资者，你必须遵循以下的问题建议:“低价购买；再低价购买”。每次你购买一支股票,你必须用低于你上次购买它的价格购买它。买的次数越多越好!你的目标是在遵循以上建议的前提下，求你最多能购买股票的次数。你将被给出一段时间内一支股票每天的出售价，你可以选择在哪些天购买这支股票。每次购买都必须遵循“低价购买；再低价购买”的原则。写一个程序计算最大购买次数。

这里是某支股票的价格清单：

$$
\def\arraystretch{1.5}
\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|c|c|}\hline
\textsf{日期} & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11 & 12 \cr\hline
\textsf{价格} & 68 & 69 & 54 & 64 & 68 & 64 & 70 & 67 & 78 & 62& 98 & 87 \cr\hline
\end{array}
$$
最优秀的投资者可以购买最多 $4$ 次股票，可行方案中的一种是：
$$
\def\arraystretch{1.5}
\begin{array}{|c|c|c|c|c|}\hline
\textsf{日期} & 2 & 5 & 6 & 10 \cr\hline
\textsf{价格} & 69 & 68 & 64 & 62 \cr\hline
\end{array}
$$

输入格式

第一行共一个整数 $N\ (1 \le N \le 5000)$，股票发行天数

第二行一行 $N$ 个整数，是每天的股票价格。保证是大小不超过 $2^{16}$ 的正整数。

输出格式

输出共一行两个整数，分别为最大购买次数和拥有最大购买次数的方案数（数据保证 $ \le 2^{31}$）当二种方案“看起来一样”时（就是说它们构成的价格队列一样的时候）,这 $2$ 种方案被认为是相同的。

样例输入 #1

12
68 69 54 64 68 64 70 67 78 62 98 87

样例输出 #1

4 2

思路

令f[i]表示以数字a[i]结尾且长度为dp[i]的方案数，那么当a[i]!=a[j]时，出现dp[i]=dp[j]+1的情况，直接在**f[i]加上f[j]，但当a[j]=a[i]时，因为我们对f[i]的定义可得，f[i]和f[j]**此时是有重合的，也就是说只保留一个最多方案的f[i]即可

最后遍历一遍数组，加上所有等于答案长度的方案数即可

#include<bits/stdc++.h>
using namespace std;
//#define int long long
const int N=1e5+10;
const int mod=1e9+7;
int dp[N],a[N];
int f[N];
void solve()
{
    int n;
    cin>>n;
    for(int i=1;i<=n;i++){
          cin>>a[i];
          dp[i]=f[i]=1;
    }
    int ans1=1;
    for(int i = 2; i <= n; i++) {
          for(int j = 1; j < i; j++){
               if(a[i] < a[j]) {
                    if(dp[i]<dp[j]+1){
                         dp[i] = max(dp[i], dp[j] + 1);
                         f[i]=f[j];
                    }
                    else if(dp[i]==dp[j]+1) f[i]+=f[j];
               }
               if(a[i]==a[j]) dp[j]=f[j]=0;
          }
          ans1 = max(ans1, dp[i]);
     }
     int num=0;
     for(int i=1;i<=n;i++){
          if(dp[i]==ans1) num+=f[i];
     }
     cout<<ans1<<' '<<num<<endl;
}
signed main()
{
    int t=1;
    //cin>>t;
    while(t--)
    {
        solve();
    }
}

同样的记录背包最优方案数在acwing有一道板题

这里用g[i]表示背包体积为i时的最优方案数

如果选第i个物品能做到让价值增加，那么舍弃掉原先的方案数，用g[j-v]的值来覆盖掉g[j];

如果选与不选对结果没有影响，即价值一样时，需要把两种状态的方案汇总到一起，g[j]+=g[j-v];

最后的g[V]即是最优情况下的方案总和

#include<bits/stdc++.h>
using namespace std;
#define int long long
const int N=2e5+10;
const int mod=1e9+7;
int dp[N];
int a[N],b[N];
int n,V;
vector<int>e[N];
int g[N];

void solve()
{
   int n,V;
   cin>>n>>V;
   for(int i=0;i<=V;i++) g[i]=1;
   for(int i=1;i<=n;i++)
   {
        int v,w;
        cin>>v>>w;
        for(int j=V;j>=v;j--)
        {
            if(dp[j]<dp[j-v]+w)
            {
                dp[j]=dp[j-v]+w;
                g[j]=g[j-v];
            }
            else if(dp[j]==dp[j-v]+w)
            {
                g[j]+=g[j-v];
                g[j]%=mod;
            }
        }
   }
   cout<<g[V]<<endl;
}
signed main()
{
    int t=1;
    //cin>>t;
    while(t--)
    {
        solve();
    }
}

• AcWing 1064. 小国王【线性状压DP+目标状态优化】
• AcWing 327. 玉米田【线性状压DP+目标状态优化】
• [NOI2001] 炮兵阵地
  • 题目描述
    • 样例输入 #1
    • 样例输出 #1

AcWing 1064. 小国王【线性状压DP+目标状态优化】

#include<bits/stdc++.h>
using namespace std;
#define int long long
const int N=1e5+10;
const int mod=1e9+7;
int n,k;
int cnt[N];
int dp[12][110][3000];
vector<int>head[N];
vector<int>state;
bool check(int st){
    for(int i=0;i<n;i++)
        if((st>>i&1)&&st>>(i+1)&1) return 0;
    return 1;
}
int count(int st){
    int res=0;
    for(int i=0;i<n;i++){
        res+=st>>i&1;
    }
    return res;
}
void solve(){
    cin>>n>>k;
    for(int i=0;i<1<<n;i++){
        if(check(i)) state.push_back(i);
        cnt[i]=count(i);
    }
    for(int i=0;i<state.size();i++){
        for(int j=0;j<state.size();j++){
            int x=state[i],y=state[j];
            if(((x&y)==0)&&check(x|y)) head[i].push_back(j);
        }
    }
    dp[0][0][0]=1;
    for(int i=1;i<=n+1;i++){
        for(int j=0;j<=k;j++){
            for(int a=0;a<state.size();a++){
                for(int b:head[a]){
                    int c=cnt[state[a]];
                    if(j>=c){
                        dp[i][j][a]+=dp[i-1][j-c][b];
                    }
                }
            }
        }
    }
    cout<<dp[n+1][k][0]<<endl;
}
signed main(){
    int t=1;
    //cin>>t;
    while(t--){
        solve();
    }
}

AcWing 327. 玉米田【线性状压DP+目标状态优化】

#include<bits/stdc++.h>
using namespace std;
#define int long long
const int N=1e5+10;
const int mod=1e8;
int n,k;
int cnt[N],a[110];
int dp[14][1<<14];
vector<int>head[1<<14];
vector<int>state;
bool check(int st){
    return !(st&st<<1);
}
int count(int st){
    int res=0;
    for(int i=0;i<n;i++){
        res+=st>>i&1;
    }
    return res;
}
void solve(){
    int n,m;
    cin>>n>>m;
    for(int i=1;i<=n;i++){
        for(int j=1;j<=m;j++){
            cin>>k,a[i]|=!k<<(j-1);
        }
    }
    for(int st=0;st<1<<m;st++){
        if(check(st)) state.push_back(st);
    }
    for(auto it:state){
        for(auto next_it:state){
            if(!(it&next_it)) head[it].push_back(next_it);
        }
    }
    dp[0][0]=1;
    for(int i=1;i<=n+1;i++){
        for(auto st:state){
            if(!(st&a[i])){
                for(auto next_st:head[st]){
                    dp[i][st]+=dp[i-1][next_st];
                    dp[i][st]%=mod;
                }
            }
        }
    }
    cout<<dp[n+1][0]<<endl;
}
signed main(){
    int t=1;
    //cin>>t;
    while(t--){
        solve();
    }
}

[NOI2001] 炮兵阵地

题目描述

司令部的将军们打算在 $N\times M$ 的网格地图上部署他们的炮兵部队。

一个 $N\times M$ 的地图由 $N$ 行 $M$ 列组成，地图的每一格可能是山地（用 $\texttt{H}$ 表示），也可能是平原（用 $\texttt{P}$ 表示），如下图。

在每一格平原地形上最多可以布置一支炮兵部队（山地上不能够部署炮兵部队）；一支炮兵部队在地图上的攻击范围如图中黑色区域所示：

如果在地图中的灰色所标识的平原上部署一支炮兵部队，则图中的黑色的网格表示它能够攻击到的区域：沿横向左右各两格，沿纵向上下各两格。

图上其它白色网格均攻击不到。从图上可见炮兵的攻击范围不受地形的影响。

现在，将军们规划如何部署炮兵部队，在防止误伤的前提下（保证任何两支炮兵部队之间不能互相攻击，即任何一支炮兵部队都不在其他支炮兵部队的攻击范围内），在整个地图区域内最多能够摆放多少我军的炮兵部队。

样例输入 #1

5 4
PHPP
PPHH
PPPP
PHPP
PHHP

样例输出 #1

6

#include<bits/stdc++.h>
using namespace std;
#define int long long
const int N=1e5+10;
const int mod=1e9+7;
int n,m;
char c;
int cnt[N],g[110];
int dp[2][1<<10][1<<10];
vector<int>head[N];
vector<int>state;
bool check(int st){
    return !(st&st>>1||st&st>>2);
}
int count(int st){
    int res=0;
    for(int i=0;i<m;i++){
        res+=st>>i&1;
    }
    return res;
}
void solve(){
    cin>>n>>m;
    for(int i=1;i<=n;i++){
        for(int j=1;j<=m;j++){
            cin>>c, g[i]|=(c=='H')<<(j-1);
        }
    }
    for(int st=0;st<1<<m;st++){
        if(check(st)) state.push_back(st),cnt[st]=count(st);
    }
    for(int x: state){
        for(int y: state){
            if(!(x&y)) head[x].push_back(y);
        }
    }
    for(int i=1;i<=n+2;i++){
        for(int st:state){
            if(!(st&g[i])){
                for(int p1:head[st]){
                    for(int p2:head[p1]){
                        if(!(st&p2)){
                            dp[i&1][st][p1]=max(dp[i&1][st][p1],dp[i-1&1][p1][p2]+cnt[st]);
                        }
                    }
                }
            }
        }
    }
    cout<<dp[n+2&1][0][0]<<endl;
}
signed main(){
    int t=1;
    //cin>>t;
    while(t--){
        solve();
    }
}

岩石怪物杜达生活在魔法森林中，他在午餐时收集了 N 块能量石准备开吃。

由于他的嘴很小，所以一次只能吃一块能量石。

能量石很硬，吃完需要花不少时间。

吃完第 ii块能量石需要花费的时间为 Si秒。

杜达靠吃能量石来获取能量。

不同的能量石包含的能量可能不同。

此外，能量石会随着时间流逝逐渐失去能量。

第 ii块能量石最初包含 Ei 单位的能量，并且每秒将失去 Li 单位的能量。

当杜达开始吃一块能量石时，他就会立即获得该能量石所含的全部能量（无论实际吃完该石头需要多少时间）。

能量石中包含的能量最多降低至 0。

请问杜达通过吃能量石可以获得的最大能量是多少？

输入格式

第一行包含整数 T，表示共有 T 组测试数据。

每组数据第一行包含整数 N，表示能量石的数量。

接下来 N 行，每行包含三个整数 Si,Ei,Li

输出格式

每组数据输出一个结果，每个结果占一行。

结果表示为 Case #x: y，其中 xx 是组别编号（从 1 开始），y 是可以获得的最大能量值。

数据范围

1≤T≤10
1≤N≤100
1≤Si≤100
1≤Ei≤105
0≤Li≤105

输入样例：

3
4
20 10 1
5 30 5
100 30 1
5 80 60
3
10 4 1000
10 3 1000
10 8 1000
2
12 300 50
5 200 0

输出样例：

Case #1: 105
Case #2: 8
Case #3: 500

样例解释

在样例＃1中，有 N=4 个宝石。杜达可以选择的一个吃石头顺序是：

• 吃第四块石头。这需要 5 秒，并给他 80 单位的能量。
• 吃第二块石头。这需要 5 秒，并给他 5 单位的能量（第二块石头开始时具有 30 单位能量，5 秒后失去了 25 单位的能量）。
• 吃第三块石头。这需要 100 秒，并给他 20 单位的能量（第三块石头开始时具有 30 单位能量，10 秒后失去了 10 单位的能量）。
• 吃第一块石头。这需要 20 秒，并给他 0 单位的能量（第一块石头以 10 单位能量开始，110 秒后已经失去了所有的能量）。

他一共获得了 105105 单位的能量，这是能获得的最大值，所以答案是 105。

在样本案例＃2中，有 N=3 个宝石。

无论杜达选择吃哪块石头，剩下的两个石头的能量都会耗光。

所以他应该吃第三块石头，给他提供 8 单位的能量。

在样本案例＃3中，有 N=2 个宝石。杜达可以：

• 吃第一块石头。这需要 12 秒，并给他 300单位的能量。
• 吃第二块石头。这需要 5秒，并给他 200 单位的能量（第二块石头随着时间的推移不会失去任何能量！）。

所以答案是 500。

#include<bits/stdc++.h>
using namespace std;
#define int long long
const int N=2e5+10;
const int mod=1e9+7;
int dp[N];
struct tr
{
    int s,e,l;
    bool operator < (const tr &a) const{
        return s*a.l<a.s*l;
    }
}tree[N];
int t,num=0;
void solve()
{
    int n,m=0;
    cin>>n;
    memset(dp,-127,sizeof(dp));
    dp[0]=0;
    for(int i=1;i<=n;i++)
    {
        int s,e,l;
        cin>>s>>e>>l;
        tree[i]={s,e,l};
        m+=s;
    }
    sort(tree+1,tree+1+n);
    for(int i=1;i<=n;i++)
    {
        for(int j=m;j>=tree[i].s;j--)
        {
            dp[j]=max(dp[j],dp[j-tree[i].s]+tree[i].e-tree[i].l*(j-tree[i].s));
        }
    }
    int ans=0;
    for(int i=0;i<=m;i++)
    {
        ans=max(ans,dp[i]);
    }
    cout<<"Case #"<<num<<": "<<ans<<endl;
}
signed main()
{
    cin>>t;
    while(num<t)
    {
        num++;
        solve();
    }
}

• D - Cross Explosion
  • Problem Statement
• E - Avoid K Partition
  • Problem Statement

D - Cross Explosion

Problem Statement

There is a grid with $H$ rows and $W$ columns. Let $(i, j)$ denote the cell at the $i$-th row from the top and $j$-th column from the left.
Initially, there is one wall in each cell.
After processing $Q$ queries explained below in the order they are given, find the number of remaining walls.

In the $q$-th query, you are given two integers $R_q$ and $C_q$.
You place a bomb at $(R_q, C_q)$ to destroy walls. As a result, the following process occurs.

• If there is a wall at $(R_q, C_q)$, destroy that wall and end the process.
• If there is no wall at $(R_q, C_q)$, destroy the first walls that appear when looking up, down, left, and right from $(R_q, C_q)$. More precisely, the following four processes occur simultaneously:
  • If there exists an $i \lt R_q$ such that a wall exists at $(i, C_q)$ and no wall exists at $(k, C_q)$ for all $i \lt k \lt R_q$, destroy the wall at $(i, C_q)$.
  • If there exists an $i \gt R_q$ such that a wall exists at $(i, C_q)$ and no wall exists at $(k, C_q)$ for all $R_q \lt k \lt i$, destroy the wall at $(i, C_q)$.
  • If there exists a $j \lt C_q$ such that a wall exists at $(R_q, j)$ and no wall exists at $(R_q, k)$ for all $j \lt k \lt C_q$, destroy the wall at $(R_q, j)$.
  • If there exists a $j \gt C_q$ such that a wall exists at $(R_q, j)$ and no wall exists at $(R_q, k)$ for all $C_q \lt k \lt j$, destroy the wall at $(R_q, j)$.

#include <bits/stdc++.h>
#define fi first
#define se second
#define int long long

using namespace std;

typedef pair<int, int> PII;
typedef long long LL;

signed main() {
    cin.tie(0);
    cout.tie(0);
    ios::sync_with_stdio(0);

    int n, m, q;
    cin >> n >> m >> q;

    vector<set<int>> col(m + 1), lin(n + 1);
    vector<vector<bool>> st(n + 1, vector<bool>(m + 1, 0));
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= m; j++) col[j].insert(i), lin[i].insert(j), st[i][j] = 1;
    int res = n * m;
    while (q--) {
        int x, y;
        cin >> x >> y;

        if (st[x][y]) {
            res--, st[x][y] = 0;
            col[y].erase(x), lin[x].erase(y);
            continue;
        }
        auto up = col[y].upper_bound(x), down = up, left = lin[x].upper_bound(y), right = left;
        if (up != col[y].begin()) {
            up--, res--, st[*up][y] = 0;
            col[y].erase(up), lin[*up].erase(y);
        }
        if (down != col[y].end()) {
            res--, st[*down][y] = 0;
            col[y].erase(down), lin[*down].erase(y);
        }
        if (left != lin[x].begin()) {
            left--, res--, st[x][*left] = 0;
            lin[x].erase(left), col[*left].erase(x);
        }
        if (right != lin[x].end()) {
            res--, st[x][*right] = 0;
            lin[x].erase(right), col[*right].erase(x);
        }
    }

    cout << res << endl;

    return 0;
}

E - Avoid K Partition

Problem Statement

You are given a sequence $A = (A_1, A_2, \dots, A_N)$ of length $N$ and an integer $K$.
There are $2^{N-1}$ ways to divide $A$ into several contiguous subsequences. How many of these divisions have no subsequence whose elements sum to $K$? Find the count modulo $998244353$.

Here, “to divide $A$ into several contiguous subsequences” means the following procedure.

• Freely choose the number $k$ $(1 \leq k \leq N)$ of subsequences and an integer sequence $(i_1, i_2, \dots, i_k, i_{k+1})$ satisfying $1 = i_1 \lt i_2 \lt \dots \lt i_k \lt i_{k+1} = N+1$.
• For each $1 \leq n \leq k$, the $n$-th subsequence is formed by taking the $i_n$-th through $(i_{n+1} - 1)$-th elements of $A$, maintaining their order.

Here are some examples of divisions for $A = (1, 2, 3, 4, 5)$:

• $(1, 2, 3), (4), (5)$
• $(1, 2), (3, 4, 5)$
• $(1, 2, 3, 4, 5)$

#include <bits/stdc++.h>
#define fi first
#define se second
#define int long long

using namespace std;

typedef pair<int, int> PII;
typedef long long LL;

const int mod = 998244353;

signed main() {
    cin.tie(0);
    cout.tie(0);
    ios::sync_with_stdio(0);

    int n, k;
    cin >> n >> k;

    vector<int> a(n + 1), s(n + 1, 0);
    for (int i = 1; i <= n; i ++)
        cin >> a[i], s[i] = s[i - 1] + a[i];

    vector<int> dp(n + 1, 0);
    unordered_map<int, int> tot;
    dp[0] = 1, tot[0] = 1;
    int sum = 1;
    for (int i = 1; i <= n; i ++) {
        dp[i] = (sum - tot[s[i] - k] + mod) % mod;
        (sum += dp[i]) %= mod, (tot[s[i]] += dp[i]) %= mod;
    }

    cout << dp[n] << endl;

    return 0;
}

E-ACM中的CM题

现在在你前面有 nnn 个地雷

刚刚学会瞬移的你决定排走所有地雷

遗憾的是，你的初始排雷能力 m=0m = 0m=0，但你知道

当排雷能力为 mmm 时，你可以任何时刻在当前位置 lll 处将[l,l+m][l, l+m][l,l+m] 中的雷全部排走

也可以在任何时刻任何地点，将排雷能力从 mmm 变为 m+1m+1m+1

以上两种操作都需要花费 1 的时间，但瞬移不花费时间！

求排所有雷所需最小时间！

思路

枚举m长度二分求次数即可

#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N = 2e5 + 10;
int a[N];
int n, ans;
void check(int len) {
    int res = len - 1;
    for (int i = 1; i <= n; i++) {
        int l = i, r = n;
        while (l < r) {
            int mid = (l + r + 1) / 2;
            if (a[mid] - a[i] + 1 > len)
                r = mid - 1;
            else
                l = mid;
        }
        res++;
        i = l;
        if (l == n)
            break;
    }
    ans = min(ans, res);
}

void solve() {
    int num;
    cin >> num;
    n = 0;
    map<int, int> mp;
    for (int i = 1; i <= num; i++) {
        int x;
        cin >> x;
        if (!mp[x]) {
            a[++n] = x;
        }
        mp[x] = 1;
    }
    ans = n;
    sort(a + 1, a + 1 + n);
    for (int i = 1; i <= n; i++) {
        check(i);
    }
    cout << ans << endl;
}
signed main() {
    int t = 1;
    while (t--) {
        solve();
    }
    return 0;
}